在進行貪婪演算法時，他採取step by step的前進模式，並在每一步中做當下最好的決策，而且不會回頭。對於greedy algorithm來說，最好的greedy rule是找出minf(i)，最短的結束時間。

在貪婪演算法裡如果我們要處理的事Interval Scheduling，我們只有一個資源可以安排整個排程，則uncompatiable的工作事項都會被捨棄，來妥善運用所擁有的資源。

note:compatiablity checking s(i)<f(i)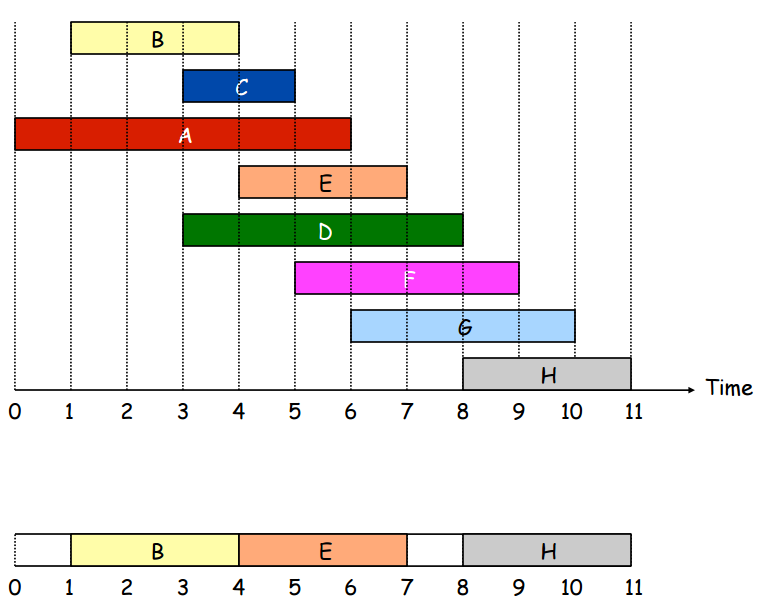

而在Interval Partitioning里，我們期望在完成所有的工作項目(Request)之下，消耗最小的資源(Resource)。一般我們將one source以一種顏色來表示。在探討這個問題的過程中，我們要介紹一個新的專有名詞Depth，他表示overlap的最大重疊數量，他相當於告訴我們至少(lower bound)需要幾個resource。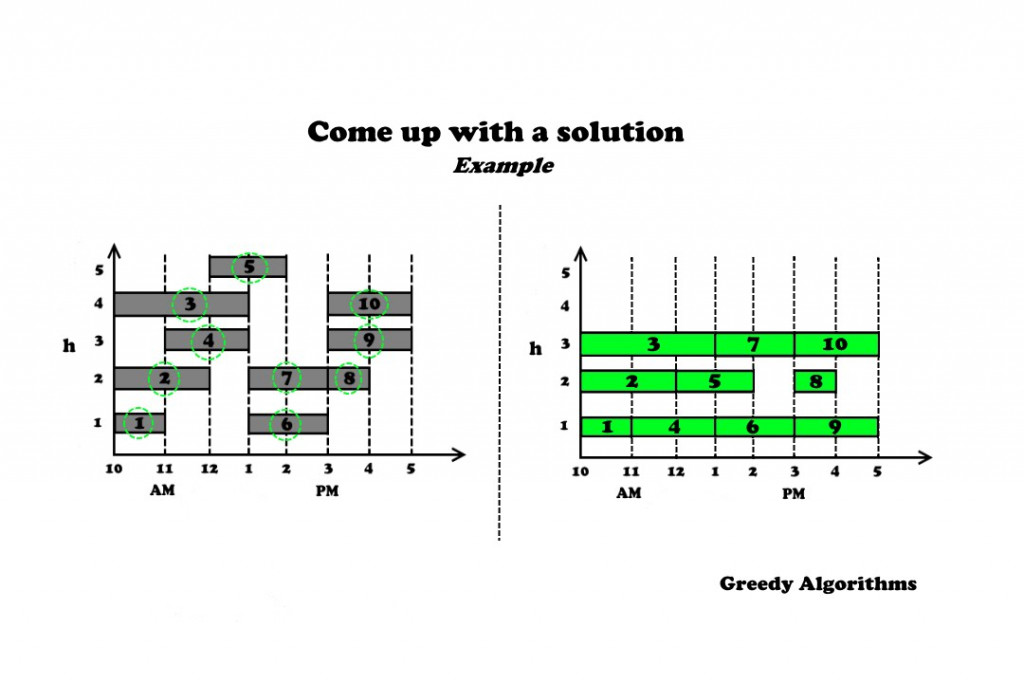

接著來介紹應用的場景：

最小生成樹問題

1. Kruskal算法

Kruskal算法是一種基於邊的貪婪演算法，用於找到圖的最小生成樹。其基本思想是按邊的權重從小到大進行排序，然後依次選擇不會形成環的最小權重邊，直到構建出一棵包含所有頂點的樹。Kruskal算法的實現通常使用並查集（Union-Find）來檢查是否形成環。

步驟：

1. 將圖中的所有邊按權重從小到大排序。
2. 從最小的邊開始，依次檢查該邊是否形成環。若不形成環，則將該邊加入生成樹。
3. 重複此過程直到生成樹包含所有頂點。

時間複雜度： (O(E \log E))，其中 (E) 是圖中的邊數。

2. Prim算法

Prim算法是另一種貪婪演算法，它從一個初始頂點開始，逐步擴展生成樹。每次將不在生成樹中的、最接近生成樹的頂點加入，並選擇相應的最小權重邊。Prim算法的實現通常使用最小優先佇列來高效地選擇最小邊。

步驟：

1. 從任意一個頂點開始，將該頂點標記為訪問過的，並將與之相連的所有邊加入一個優先佇列。
2. 每次從優先佇列中選擇權重最小的邊，將與該邊相連且未訪問過的頂點加入生成樹，並更新與該頂點相連的邊。
3. 重複這個過程直到所有頂點都被訪問。

時間複雜度： (O((V + E) \log V))，其中 (V) 是頂點數，(E) 是邊數。

單源最短路徑問題

Dijkstra算法

Dijkstra算法是一種用於計算單源最短路徑的貪婪演算法。它在圖中逐步擴展最短路徑樹，每次選擇當前最小距離的未處理頂點，並更新其鄰居的距離。Dijkstra算法通常也使用優先佇列來高效選擇距離最小的頂點。

步驟：

1. 初始化所有頂點的距離為無限大，起始頂點的距離設為0。將所有頂點標記為未處理。
2. 從未處理的頂點中選擇距離最小的一個，標記其為處理過的。
3. 更新該頂點的所有鄰居的距離，如果通過該頂點可以得到更小的距離，則更新鄰居的最短距離。
4. 重複此過程直到所有頂點都被處理。

時間複雜度： (O((V + E) \log V))，與Prim算法相似。

活動選擇問題

活動選擇問題

活動選擇問題的目標是在一組活動中選擇最多的不重疊活動，這是一個典型的貪婪算法應用場景。活動選擇問題可以在 (O(n \log n)) 的時間內解決，這裡 (n) 是活動數量。

步驟：

1. 將所有活動按結束時間從早到晚排序。
2. 從最早結束的活動開始選擇，將其加入到解中。
3. 對於每個後續活動，如果它的開始時間晚於或等於已選活動的結束時間，則選擇該活動。
4. 重複此過程直到所有活動都被考慮。

分數背包問題

分數背包問題

分數背包問題是一個經典的貪婪算法應用，目的是在背包容量有限的情況下，最大化放入背包的物品的總價值。與0/1背包問題不同的是，這裡的物品可以被部分放入背包。分數背包問題的貪婪算法保證能夠找到全局最優解。

步驟：

1. 將所有物品按價值密度（即價值與重量的比值）從高到低排序。
2. 從價值密度最高的物品開始，盡可能多地將其放入背包。
3. 如果某一物品不能完整放入背包，則放入其部分，直到背包容量滿為止。

時間複雜度： (O(n \log n))，其中 (n) 是物品數量。